一个密钥是一个长度为 $n = 2k+1$ 的字符串,它包含 $1$ 个字母X、$k$ 个字母 A 和 $k$ 个字母 B。例如 $k=3$ 时,BAXABAB 就是一个密钥。
如下图所示,可以按顺时针顺序把这 $2k+1$ 个字母排成一个圈:
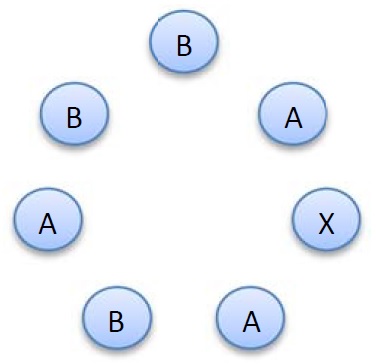
在 $k$ 个字母 A 中,有一部分可以定义为"强的"。
具体来说,从 X 出发顺时针走到某个 A 时,如果途中 A 的数目严格多于 B 的数目,则称此字母 A 为强的。
对于上面的例子来说,顺时针方向从字母 X 数起第 $1$ 个和第 $2$ 个字母 A 是强的,而第 $3$ 个字母 A 不是强的。
一个密钥的特征值就是其中包含的强的字母 A 的个数。
天才小朋友 KT 给出了一个结论:
假设 $k$ 个字母 A 所在的位置已经固定,但是剩下的 $k$ 个 B 和 $1$ 个 X 的位置是未知的。 (注意,满足这样要求的密钥一共有 $k+1$ 个,因为字母 X 还剩下 $k+1$ 个可能的位置。)
可以证明:所有这$k+1$个可能的密钥的特征值是各不相同的,它们恰好为$0,1,2,…,k$。
下页的图是一个具体的示例,从左到右的四个子图中分别有3个,2个,1个,0个字母A是强的。
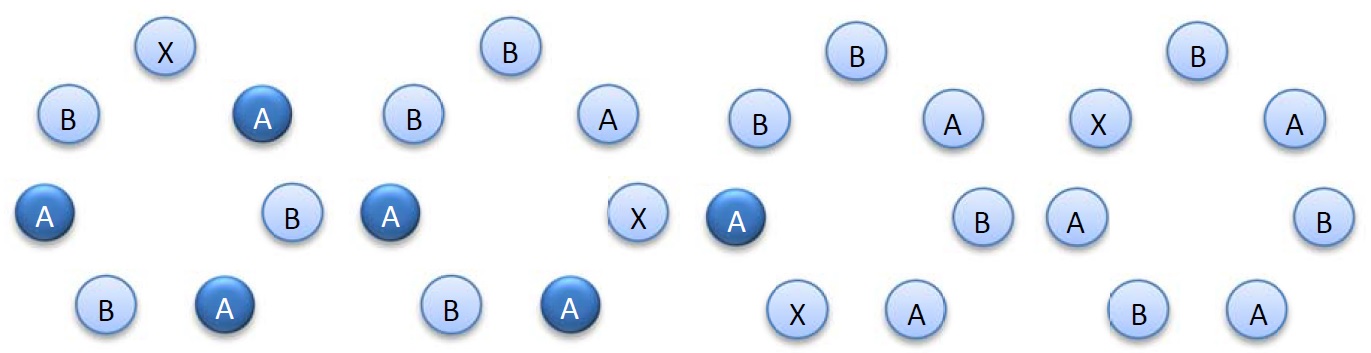
类似地,如果固定 $k$ 个字母 B 的位置,那满足条件的所有 $k+1$ 个密钥的特征值也各不相同,恰好为 $0,1,\cdots,k$。
现在你需要解决以下三个问题:
- 给定密钥中所有 A 的位置,当密钥的特征值为 $0$ 时,请问 X 在哪个位置。
- 给定密钥中所有 A 的位置,当密钥的特征值为 $S$ 时,请问 X 在哪个位置。
- 给定密钥中所有 B 的位置,当密钥的特征值为 $S$ 时,请问 X 在哪个位置。
注意:字符串的 $2k+1$ 个字母的位置由 $1$ 到 $2k+1$ 编号。
例子一
假定 $k=3,S=2$。那么:
当 A 的位置是 $\{2,4,6\}$ 且特征值为 $0$ 时,X 的位置在 $7$;
当 A 的位置是 $\{2,4,6\}$ 且特征值为 $2$ 时,X 的位置在 $3$;
当 B 的位置是 $\{2,4,6\}$ 且特征值为 $2$ 时,X 的位置在 $5$。
例子二
假定 $k=9,S=7$。那么:
当 A 的位置是 $\{3,4,5,9,10,12,13,16,19\}$ 且特征值为 $0$ 时,X 的位置在 $14$;
当 A 的位置是 $\{3,4,5,9,10,12,13,16,19\}$ 且特征值为 $7$ 时,X 的位置在 $18$;
当 B 的位置是 $\{3,4,5,9,10,12,13,16,19\}$ 且特征值为 $7$ 时,X 的位置在 $17$。
输入格式
只包含一组测试数据。
第一行包含一个整数$k$,意义如题所述。
第二行包含一个整数$seed$,这个数将用于生成一个$k$元集合P。
第三行包含一个整数$S$,意义如题所述。
保证$0\le S \le k \le 10^7$。$1\le seed \le 10000$。
在下发文件中,包含三个用于生成输入数据的文件cipher.cpp/c/pas。其中读入部分已经完成,在数组 $p[]$ 中,若 $p[i]= 0$,表示 $i$ 不属于集合$P$,否则,$i$ 属于集合 $P$。
输出格式
输出三行,每行一个数,依次对应问题描述中的三个子问题的答案。
即:
- 第一个数表示当 $k$ 元集合 $P$ 代表 A 的位置且特征值为 $0$ 时 X 的位置。
- 第二个数表示当 $k$ 元集合 $P$ 代表 A 的位置且特征值为 $S$ 时 X 的位置。
- 第三个数表示当 $k$ 元集合 $P$ 代表 B 的位置且特征值为 $S$ 时 X 的位置。
样例一
input
5 3344 2
output
10 1 2
explanation
第一个样例中,$P$ 数组为 $1$ 的元素的下标分别为 $5,6,7,8,9$。
样例二
input
500000 4545 234567
output
999992 246922 753067
限制与约定
对于 $30\%$ 的数据,$k \le 10^3$。
对于 $50\%$ 的数据,$k \le 10^5$。
对于 $100\%$ 的数据,$k \le 10^7$。
对于每个测试点,得分为以下三部分得分之和:
- 如果第一问回答正确,你将获得 $3$ 分。
- 如果第二问回答正确,你将获得 $4$ 分。
- 如果第三问回答正确,你将获得 $3$ 分。
如果你仅仅知道部分答案,请也务必按此格式要求输出三个数。否则你可能会因格式错误无法得分。