之前看到彬皓在 $T1$ 的三角函数上面可以获得 $100pts$ 的好成绩，但是我的伪 “三角函数” 的分数只有 $70pts.$ 彬皓和我同为初二学生，他却可以写过去 ，让人佩服。

所以要学习三角函数弥补我在计算几何上面的过失。说实话这东西鸽了很久很久很久了。

发现整个机房就我一个人没了解过向量，将三角函数的时候就我一个人不会。

所以这个东西确实应该补一补。

正好我有一个老掉牙的 $\text{geogebra}.$ 万事俱备只欠东风。

向量及其定义

向量是一种具有方向也具有大小的量。在这里向量的起点为 $A$ ，终点为 $B$ ，那么这个向量可以被表示为 $\overrightarrow{AB}.$ 或者可以用一个小写字母 $a$ 表示，表示为 $\vec{a}$ ，还可以表示为 $\bf{a}$ （这东西为什么不是斜体）

通常认为向量的起点均为原点 $O$，原点的坐标是 $(0,0)$ ，终点是向量平移到起点和原点重合时的原点。

向量的模

可以简单地理解为向量的长度。设这个向量的终点是 $(x,y)$，那么向量的模长是 $\sqrt{ x^2 + y^2 }.$

向量 $a$ 的模记作 $|a|.$

两点 $(x_1,y_1),(x_2,y_2)$ 之间的距离是 $\sqrt{(y_1-x_1)^2+(y_2-x_2)^2}.$ 考虑到向量的起点是原点，所以向量模长可以简单地得到。

后面可以发现向量的模长和绝对值很像，因为有 $|-\vec{a}|=|\vec{a}|.$

相反向量

记 $-\vec{a}$ 为向量 $\vec{a}$ 的相反向量。

也就是向量在从原点 $\cal{O}$ 反向延长这个向量的模之后得到的以原点为起点的向量。（顺口编的）

从上面的定义可以推导到：

设 $\vec{a}=(x,y)$ ，则有 $-\vec{a}=(-x,-y).$ 由定义得，$|-\vec{a}|=|\vec{a}|.$

向量加和

向量 $\vec{a}+\vec{b}.$

几何意义：移动 $\vec{b}$ ，使 $\vec{b}$ 的起点与 $\vec{a}$ 的终点相重合，则从原点为起点，以 $\vec{b}$ 为终点的向量是 $\vec{a}+\vec{b}.$

设 $\vec{a}=(x_1,y_1)$ ，$\vec{b}=(x_2,y_2)$ ， 则 $\vec{a}+\vec{b}=(x_1+x_2,y_1+y_2).$

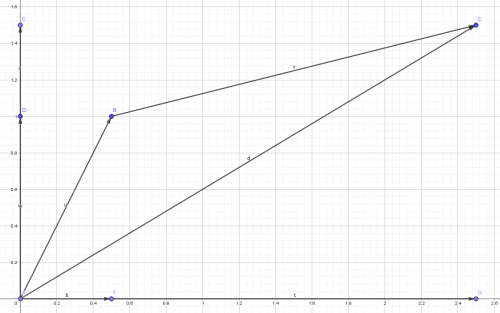
$\cal{PS : }$ 不知道怎么放大字母大小

向量相减：向量 $\bf{b}$ 的加法逆元是 $-\bf{b}$ ，计算 $a+(-\bf{b})$ 就好了。是至于加法逆元的计算见相反向量。

注意向量的模长之和不与两个向量模长成加和的关系，即

有 $\vec{a}+\vec{b}=\vec{c}$ ，不一定有 $|\vec{a}|+|\vec{b}|=|\vec{c}|$ 原因还是参见上面的图。

大概是为数不多的允许向量移动。

向量点积

放缩。$\lambda \vec{a}.$

几何意义：以 $\lambda$ 倍数放缩 $\vec{a}$，得到 $\lambda \vec{a}.$

设 $\vec{a}=(x,y)$ ， 有 $\lambda \vec{a}=(\lambda x,\lambda y).$