题目背景
Syzygy,中文译作朔望,表示三个或三个以上的天体大致位于同一直线上。本题中主要探讨母恒星与至少两颗行星位于同一直线上的情况。
题目描述
在一个理想的行星系中,所有行星在同一平面内围绕共同的单一母恒星作匀速圆周的公转运动,且公转方向相同(如同为逆时针)。我们定义这样的行星系的 Syzygy 指数为平均每年发生的所有(含母恒星的)朔望的稀有程度之和,其中单次朔望的稀有程度是与产生连线的行星数量 $x$ 有关的常数 $w_x$;如果在行星系中同时发生多个朔望但不位于同一直线上,则对每条直线上的行星分别统计稀有程度。
现有一理想的包含 $n$ 颗行星的行星系,其中从内到外第 $i$ 颗行星绕母恒星公转周期为 $t_i$ 年(根据开普勒第三定律可知 $t_i$ 单调递增)。假设存在某一时刻,所有 $n$ 颗行星位于同一条以母恒星为端点的射线上。请求出该系统的 Syzygy 指数。
输入格式
从标准输入读入数据。
第一行输入一个正整数 $n$($2\le n\le 20$),表示该单星系统中行星的数量。
第二行输入 $n$ 个正整数 $t_1, t_2, \cdots, t_n$,分别表示公转轨道从内到外各行星的公转周期。保证 $1\le t_1 < t_2 < \cdots < t_n\le 10^9$。
第三行输入 $(n-1)$ 个正整数 $w_2, w_3, \cdots, w_n$($1\le w_i\le 10^9$),分别表示发生不同数量的行星参与的朔望的稀有程度。
输出格式
输出到标准输出。
输出该行星系的 Syzygy 指数。显然 Syzygy 指数是一个有理数;不妨假设其化为最简分式后的形式为 $p/q$(即其中 $p, q$ 互质),请输出 $x$ 使得 $qx\equiv p \pmod{10^9 + 7}$ 且 $0\le x < 10^9 + 7$。可以证明,在本题数据范围下,$x$ 存在且唯一。
样例
输入
2
3 4
5输出
833333340解释
不妨假设 $T=0$ 时刻两颗行星位于同一以母恒星为端点的射线上。由于两颗行星的公转周期的最小公倍数为 $12$ 年,且两颗行星的会合周期也恰为 $\displaystyle\frac{1}{\displaystyle\left|\frac{1}{3}-\frac{1}{4}\right|}=12$ 年,故可取 $T\in[0, 12)$ 年的行星系的运行情况作为研究对象。$T$ 取 $[0, 12)$ 中整数值时,行星系的运行情况分别如下各图所示:
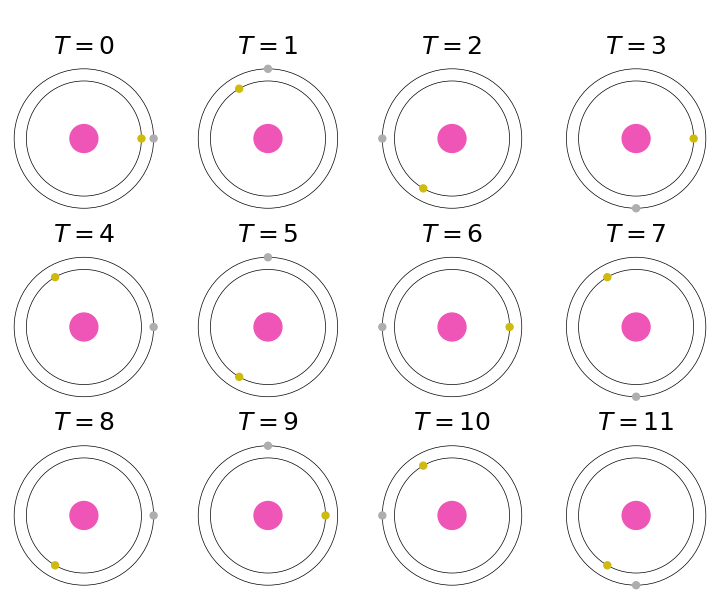
可以证明,在 $12$ 年的周期内,两颗行星仅发生如上图所示的 $2$ 次朔望(分别为 $T=0$ 时的内行星凌/外行星冲及 $T=6$ 年的合)。因此,该行星系的 Syzygy 指数为
$$ \frac{2\times 5}{12} = \frac{5}{6} \equiv 833333340 \pmod{10^9 +7}. $$
样例
输入
3
4 5 6
7 8输出
300000004解释
同理设 $T=0$ 时刻三颗行星位于同一以母恒星为端点的射线上。由 $\mathrm{lcm}(4, 5, 6)=60$,可取 $T\in[0,60)$ 年的行星系的运行情况作为研究对象。在这段时间内,发生的所有含母恒星的朔望如下图所示:
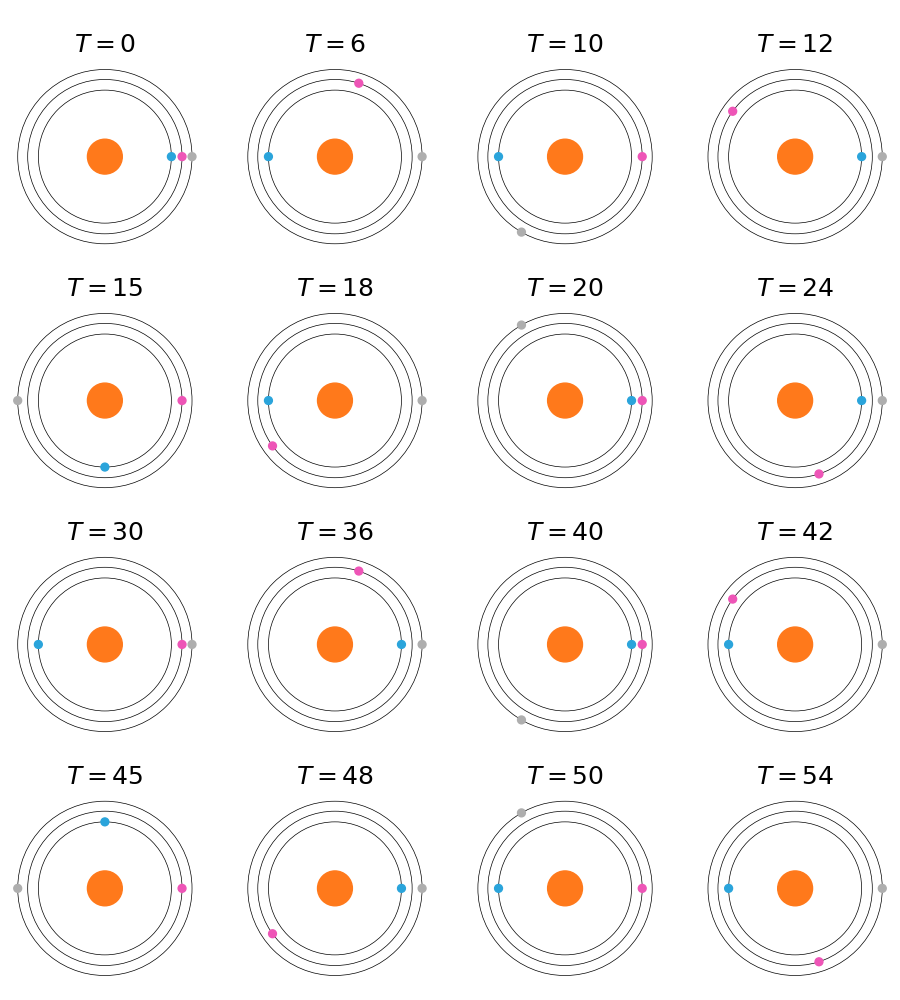
因此,该行星系的 Syzygy 指数为
$$ \frac{14\times 7+2\times 8}{60}=\frac{19}{10}\equiv300000004 \pmod{10^9+7}. $$
样例
输入
4
4 6 8 24
20 22 1207输出
250000119解释
同理设 $T=0$ 时刻四颗行星位于同一以母恒星为端点的射线上。由 $\mathrm{lcm}(4, 6, 8, 24)=24$,可取 $T\in[0,24)$ 年的行星系的运行情况作为研究对象。在这段时间内,发生的所有含母恒星的朔望如下图所示:
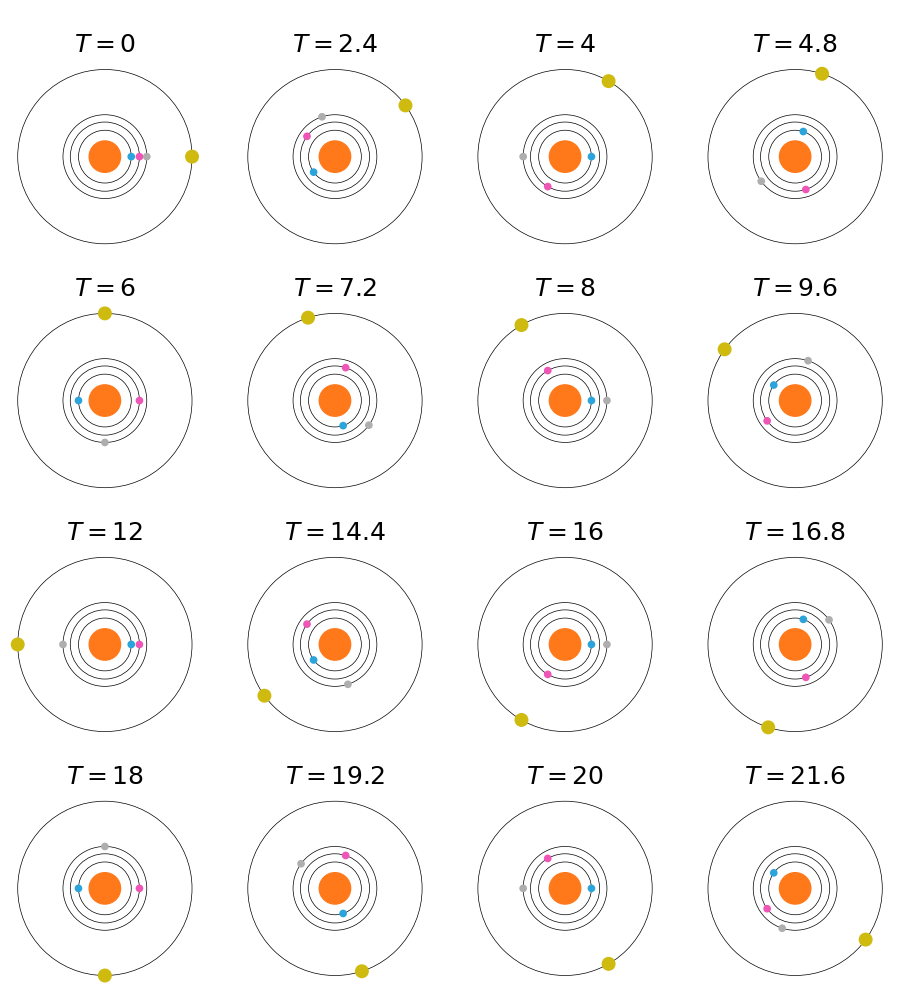
因此,该行星系的 Syzygy 指数为
$$ \frac{20\times 20+0\times22+2\times 1207}{24}=\frac{1407}{12}\equiv250000119 \pmod{10^9+7}. $$
样例
输入
9
88 225 365 687 4333 10759 30685 60189 90560
306 241 336 406 342 86884 86885 86886输出
94380764