题目描述
小 A 和小 S 是 ACM 队友。小 A 的眼睛很大、视力出众,往往能从数据中看出奇怪的规律。
某次训练,小 S 在纸上画了个圆。小 A 看了一眼,说:你这明明是正 17 边形啊!他又拿出许多正多边形图片,让小 S 观察。但小 S 对此毫无头绪,于是他请你帮忙鉴定一下。
具体来说,给定多边形最大边数 n,小 A 采用以下方式生成了平面上的 N 个点:
- 首先,选取一个点 (x,y) 作为中心。这个点可能固定为 (0,0),也可能是在 [−1,1]×[−1,1] 中均匀选取的。
- 随机在 [max 中选取一个整数 k。
- 考虑以 (x, y) 为圆心, 1 为半径的圆。均匀随机选取圆的一个内接正 k 边形。
- 重复 N 次,每次均匀随机选取正 k 边形边界上的一点 u,并把 \hat u=u+\mathcal N 加入到数据中。这里,\mathcal N 是一个随机噪声,其两维坐标分别独立遵循以 0 为均值,0.01 为标准差的高斯分布。
- 以上所有随机过程独立。
你需要从这 N 个点中,还原出多边形的边数 k。
输入格式
从标准输入读入数据。
本题有多组测试数据。第一行输入正整数 T,表示测试数据组数。
对于每组数据,第一行输入两个正整数 N,n,表示点数和多边形边数的最大可能值。之后 N 行,每行两个浮点数 \hat u_x, \hat u_y,表示一个点 \hat u 的坐标。输入中所有浮点数均保留 6 位有效数字。
输出格式
输出到标准输出。
对于每组数据,输出一个 k 表示多边形的边数。
样例一
见下发文件。
解释
以下分别是样例第 2,4,5,8 组数据的可视化图像。
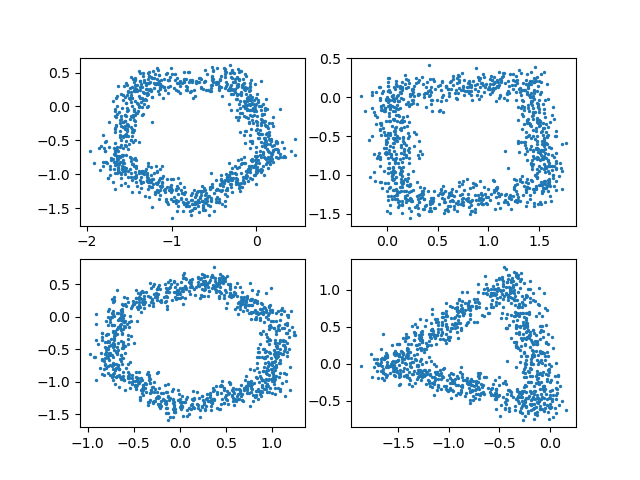
子任务
对于所有测试点,T=200,N=1000,3 \le n \le 30。
本题共十个测试点,每个测试点十分,不捆绑测试。
| 测试点编号 | n \le | 中心的选取方式 |
|---|---|---|
| 1 | 4 | 在 [-1,1] \times [-1,1] 中均匀选取$ |
| 2 | 固定为 (0,0) | |
| 3 | 10 | 在 [-1,1] \times [-1,1] 中均匀选取 |
| 4 | 固定为 (0,0) | |
| 5 | 20 | 在 [-1,1] \times [-1,1] 中均匀选取 |
| 6 | 固定为 (0,0) | |
| 7 | 25 | 在 [-1,1] \times [-1,1] 中均匀选取 |
| 8 | 固定为 (0,0) | |
| 9 | 30 | 在 [-1,1] \times [-1,1] 中均匀选取 |
| 10 | 固定为 (0,0) |
评分方式
对于每个测试点,若你在至多一组测试数据上答案错误,可以获得全部分数,否则不能获得任何分数。
提示
你可能需要以下数学定义,但无法理解以下内容并不影响你的解题:
一个随机变量 X 遵循均值为 \mu、标准差为 \sigma 的高斯分布 \mathcal N(\mu, \sigma^2) 意味着其概率密度函数为 f(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}. 对于一个概率密度函数为 f(x) 的连续随机变量 X 以及实数 a < b,随机变量 X 生成的随机数落在区间 (a,b) 的概率为 \Pr(X \in (a,b)) = \int_a^b f(x) dx.
你可能需要以下问题性质:
高斯分布的特点为:其密度从均值往左右以指数速度下降,因此在标准差较小的情况下,随机变量的值高概率与均值相近。例如,在本题的情境中,\mu = 0,\sigma = 0.01,生成出的随机数的绝对值大于 0.04 的概率约为 6 \times 10^{-4},大于 0.05 的概率不超过 6 \times 10^{-7},大于 0.07 的概率不超过 3 \times 10^{-12}。