After discovering $n$ planets, numbered from $0$ to $n-1$, the Pharaohs have started to build a transportation system between them by one-way teleporters. Each teleporter has a starting planet and an ending planet. When a tourist uses a teleporter in the starting planet, the tourist is teleported to the ending planet. Note that the starting and ending planet of a teleporter may be the same. A teleporter with its starting planet $u$ and ending planet $v$ is denoted by $(u,v)$.
To encourage widespread use of the teleportation system, the Pharaohs have created a game that can be played by tourists while travelling with the transportation system. A tourist can start the game from any planet. The planets $0, 1, \ldots, k-1$ ($k \leq n$) are called special planets. Every time a tourist enters a special planet, the tourist gets an stamp.
Currently, for each $i$ ($0 \leq i \leq k-2$), there is a teleporter $(i, i+1)$. These $k-1$ teleporters are called starting teleporters.
New teleporters are added one by one. As new teleporters are added, it may become possible for a tourist to get infinite number of stamps. To be precise, this happens when there is a sequence of planets $w[0], w[1], \ldots, w[t]$ satisfying the following conditions:
- $1 \leq t$
- $0 \leq w[0] \leq k-1$
- $w[t] = w[0]$
- For each $i$ ($0 \leq i \leq t-1$), there is a teleporter $(w[i], w[i+1])$.
Note that a tourist can use starting teleporters and any teleporters that have been added so far.
Your task is to help the Pharaohs verify, after the addition of each teleporter, whether a tourist can get infinite number of stamps or not.
Implementation details
You should implement the following procedures:
init(int n, int k)
- $n$: the number of planets.
- $k$: the number of special planets.
- This procedure is called exactly once, before any calls to
add_teleporter.
int add_teleporter(int u, int v)
- $u$ and $v$: the starting and the ending planet of the added teleporter.
- This function is called at most $m$ times (for the value of $m$, see Constraints).
- This function should return $1$ if, after the teleporter $(u,v)$ is added, the tourist can get infinite number of stamps. Otherwise, this function should return $0$.
- Once this function returns $1$, your program will be terminated.
Examples
Example 1
Consider the following call:
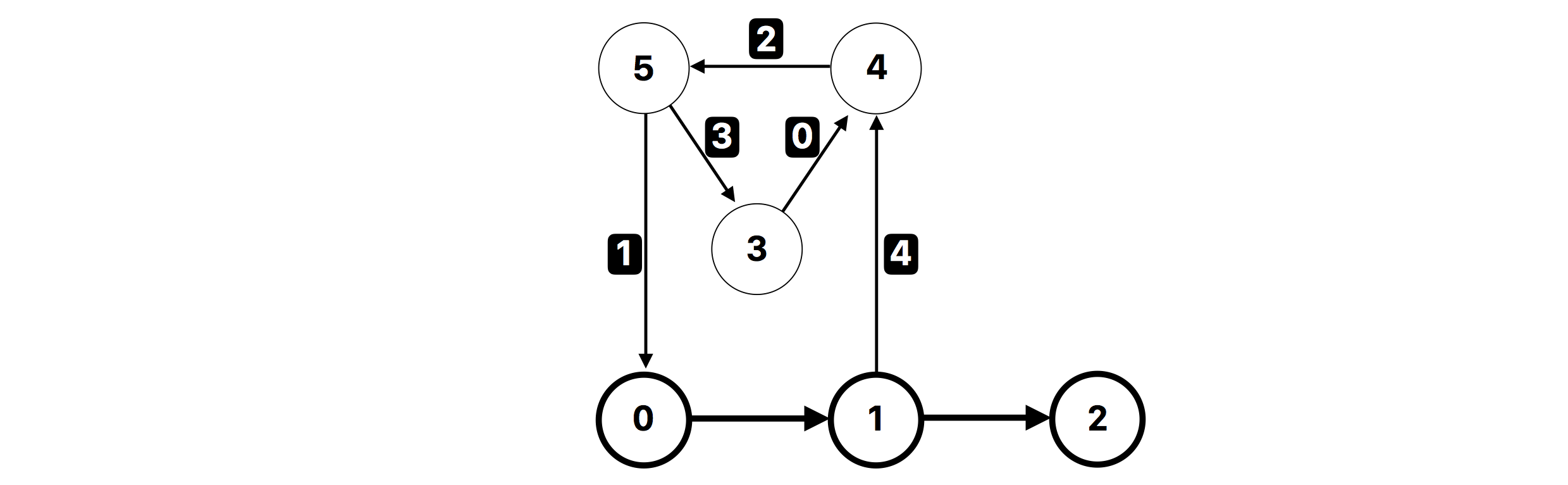
init(6, 3)
In this example, there are $6$ planets and $3$ special planets. The planets $0$, $1$, and $2$ are special planets. The starting teleporters are $(0, 1)$ and $(1, 2)$.
Suppose that the grader calls:
- (0)
add_teleporter(3, 4): You should return $0$. - (1)
add_teleporter(5, 0): You should return $0$. - (2)
add_teleporter(4, 5): You should return $0$. - (3)
add_teleporter(5, 3): You should return $0$. - (4)
add_teleporter(1, 4): At this point it is possible to get infinite number of stamps. For example, the tourist starts in the planet $0$, goes to the planets $1, 4, 5, 0, 1, 4, 5, 0, \ldots$ in this order. Hence, you should return $1$, and your program will be terminated.
The following figure illustrates this example.
The special planets and the starting teleporters are shown in bold.
Teleporters added by add_teleporter are labeled from $0$ through $4$, in order.
Example 2
Consider the following call:
init(4, 2)
In this example, there are $4$ planets and $2$ special planets. The planets $0$ and $1$ are special planets. The starting teleporter is $(0, 1)$.
Suppose that the grader calls:
add_teleporter(1, 1): after adding the teleporter $(1,1)$, it is possible to get infinite number of stamps. For example, the tourist starts in the planet $1$, and enters the planet $1$ infinitely many times using the teleporter $(1,1)$. Hence, you should return $1$, and your program will be terminated.
Another sample input/output is also available in the attachment package.
Constraints
- $1 \leq n \leq 300\,000$
- $1 \leq m \leq 500\,000$
- $1 \leq k \leq n$
For each call to the add_teleporter procedure:
- $0 \leq u \leq n-1$ and $0 \leq v \leq n-1$
- There is no teleporter from the planet $u$ to the planet $v$ before adding the teleporter $(u,v)$.
Subtasks
- (2 points) $n = k$, $n \leq 100$, $m \le 300$
- (10 points) $n \leq 100$, $m \le 300$
- (18 points) $n \leq 1\,000$, $m \leq 5\,000$
- (30 points) $n \leq 30\,000$, $m \leq 50\,000$, $k \leq 1\,000$
- (40 points) No additional constraints
Sample grader
The sample grader reads the input in the following format:
- line $1$: $\,\, n\,m\,k$
- line $2 + i$ ($0 \leq i \leq m-1$): $\,\, u[i]\,v[i]$
The sample grader first calls init, and then add_teleporter for $u = u[i]$ and $v = v[i]$ for $i = 0, 1,\ldots,m-1$ in order.
It prints the index of the first call to add_teleporter which returns $1$ (which is between $0$ and $m-1$, inclusive), or $m$ if all calls to add_teleporter return $0$.
If some call to add_teleporter returns an integer other than $0$ or $1$, the sample grader prints $-1$ and your program is terminated immediately.# Game
After discovering $N$ planets, numbered from $0$ to $N-1$, Pharaos has started to build a transportation system between them by one-way teleporters. Each teleporter has a starting planet and an ending planet. When a tourist uses a teleporter in the starting planet, the tourist is teleported and enters the ending planet. Note that the starting and ending planet of a teleporter may be the same. A teleporter with its starting planet $u$ and ending planet $v$ is denoted by $(u,v)$.
To encourage widespread use of the teleportation system, Pharaos has created a game that can be played by tourists travelling from planet to planet with the transportation system. A tourist can start the game from any planet. The planets $0, 1, \ldots, K-1$ ($K \leq N$) are called special planets. Every time a tourist enters a special planet, the tourist gets an stamp.
Currently, for each $i$ ($0 \leq i \leq K-2$), there is a teleporter $(i, i+1)$. These $K-1$ teleporters are called starting teleporters.
New teleporters are added one by one. As new teleporters are added, it may become possible for a tourist to get infinite number of stamps. To be precise, this happens when there is a sequence of planets $w\_0, w\_1, \ldots, w\_t$ satisfying the following conditions:
- $1 \leq t$
- $0 \leq w\_0 \leq K-1$
- $w\_t = w\_0$
- For each $i$ ($0 \leq i \leq t-1$), there is a teleporter $(w\_i, w\_{i+1})$.
Note that a tourist can use starting teleporters and any teleporters that have been added so far.
Your task is to help Pharaos verify, after the addition of each teleporter, whether a tourist can get infinite number of stamps or not.
Implementation details
You should implement the following procedure and function:
init(int N, int K)
N: the number of planets.K: the number of special planets.- This procedure is called exactly once, before any calls to
add_teleporter.
The following function is called for each teleporter addition.
int add_teleporter(int u, int v)
uandv: the starting and the ending planet of the added teleporter.- This function is called at most $M$ times (for the value of $M$, see Constraints).
- This function should return $1$ if, after the teleporter $(u,v)$ is added, the tourist can get infinite number of stamps. Otherwise, this function should return $0$.
- Once this function returns $1$, your program will be terminated.
Examples
Example 1
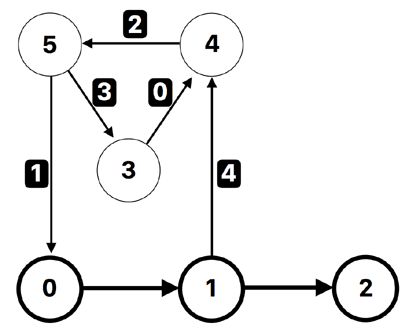
Let $N = 6$ and $K = 3$.
The grader first calls init(6, 3).
In this example, there are $6$ planets and $3$ special planets. The planets $0$, $1$, and $2$ are special planets. The starting teleporters are $(0, 1)$ and $(1, 2)$.
Suppose that the grader calls:
- (0)
add_teleporter(3, 4): You should return $0$. - (1)
add_teleporter(5, 0): You should return $0$. - (2)
add_teleporter(4, 5): You should return $0$. - (3)
add_teleporter(5, 3): You should return $0$. - (4)
add_teleporter(1, 4): At this point it is possible to get infinite number of stamps. For example, the tourist starts in the planet $0$, goes to the planets $1, 4, 5, 0, 1, 4, 5, 0, \ldots$ in this order. Hence, you should return $1$, and your program will be terminated.
The following figure illustrates this example.
The special planets and the starting teleporters are shown in bold.
Teleporters added by add_teleporter are labeled from $0$ through $4$, in order.
The file sample-01-in.txt in the zipped attachment package corresponds to this example.
Example 2
Let $N = 4$ and $K = 2$.
The grader first calls init(4, 2).
In this example, there are $4$ planets and $2$ special planets. The planets $0$ and $1$ are special planets. The starting teleporter is $(0, 1)$.
Suppose that the grader calls:
add_teleporter(1, 1): after adding the teleporter $(1,1)$, it is possible to get infinite number of stamps. For example, the tourist starts in the planet $1$, and enters the planet $1$ infinitely many times using the teleporter $(1,1)$. Hence, you should return $1$, and your program will be terminated.
The file sample-02-in.txt in the zipped attachment package corresponds to this example.
Another sample input/output are also available in the package.
Constraints
- $1 \leq N \leq 300\,000$
- $1 \leq M \leq 500\,000$
- $1 \leq K \leq N$
- $0 \leq u \leq N-1$ and $0 \leq v \leq N-1$ for any call to
add_teleporter. For any call toadd_teleporter, there is no teleporter from the room $u$ to the planet $v$ before adding the teleporter $(u,v)$.
Subtasks
- (2 points) $N = K$, $N \leq 100$, $M \le 300$
- (10 points) $N \leq 100$, $M \le 300$
- (18 points) $N \leq 1\,000$, $M \leq 5\,000$
- (30 points) $N \leq 30\,000$, $M \leq 50\,000$, $K \leq 1\,000$
- (40 points) No additional constraints
Sample grader
The sample grader reads the input in the following format:
- line $1$: $N$ $M$ $K$
- line $2 + i$ ($0 \leq i \leq M-1$): $u_i$ $v_i$
The sample grader first calls init, and then add_teleporter for $u = u_i$ and $v = v_i$ for $i = 0, 1,\ldots,M-1$ in order.
It prints the index of the first call to add_teleporter which returns $1$ (which is between $0$ and $M-1$, inclusive), or $M$ if all calls to add_teleporter return $0$.
If some call to add_teleporter returns an integer other than $0$ or $1$, the sample grader prints $-1$ and your program is terminated immediately.