This year the winter came early. Fortunately, it’s not too harsh, but the temperatures oscillating around zero have a detrimental effect on the roads. What’s worse, it turned out that the road maintenance board is out of money, and there’s still a long time until new year (and new budget allowance). Foreseeing numerous roads to be damaged, the director of the board ordered to only repair the subset of roads of minimum total length that still allows traveling between any pair of towns. Proud of his idea he decided to call this subset a minimal support of transportation, in short MST. When Johnny, his brightest employee, mentioned that there can be more than one MST, the director promptly concluded that it’s actually quite fortunate: as long as there exists MST consisting only of undamaged roads the repairs are not necessary at all! And for the second question, which Johnny intended to be rhethorical “How many broken roads will it take until we actually start repairing them?” he just replied: “Great question! I’m waiting for an answer!”. Unfortunately this question is too hard for Johnny, so he decided to outsource it to external expert (i.e. you). During the talk with you he proudly pointed out that all the roads are bidirectional.
Input Format
The first line of input contains two integers n and m (1≤n≤300, 1≤m≤600), separated by single space and representing the number of towns and the number of bidirectional roads between those towns respectively. The next m lines describe the roads. Each of those lines contains three integers ai, bi, and ci (1≤ai,bi≤n, ai≠bi, 1≤ci≤106), separated by single spaces, which means that the towns ai and bi are directly connected by a road of length ci.
Two towns can be directly connected by more than one road, but there are no roads that would have both endpoints at the same town (such roads, if they existed, would never be repaired anyway). You can assume that given roads allow traveling between any pair of towns.
Output format
The first and only line of output should contain a single integer: the minimum possible number of roads that, if broken, would force the road maintenance board to order repairing one of them.
Sample
Input
4 5
2 3 5
3 4 5
2 4 6
1 4 2
1 2 2Output
1Notes
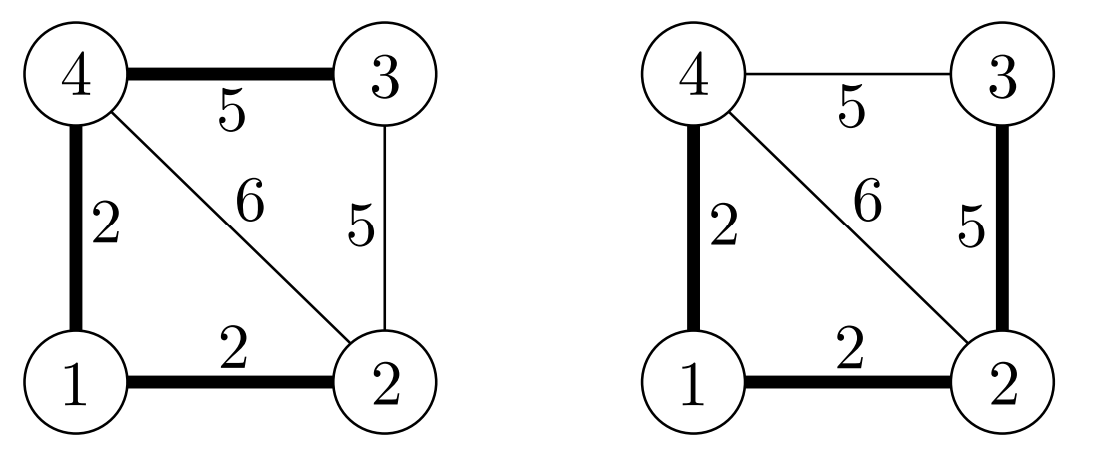
The road network from example test contains exactly two MSTs, marked with thick lines on the diagram. Both roads of length 2 belong to both MSTs, so breaking any of them forces a repair.