这是一道交互题。
跳蚤国王正在带领着四万万跳蚤造计算机。
我们给每只跳蚤一个从 $0$ 开始的整数编号。
由于跳蚤国的文明比较落后,每只跳蚤只能存储一个 $0$ 或 $1$ 的值,对于第 $i$ 只跳蚤这个值记为 $v_i$。
对于所有编号小于 $2n$ 的跳蚤,它们的值由跳蚤国王决定。即,这 $2n$ 个值可以看作是输入。
我们记 \begin{equation} F(a,b,f) = \left \lfloor \frac{f}{2 ^ {2 a + b}} \right \rfloor \mod 2 \end{equation}
对于编号大于等于 $2n$ 的每只跳蚤,设它的编号为 $i$ , 你需要给它指定三个参数 $a_i, b_i, f_i$ ($0 \le a_i < i, 0 \le b_i < i, 0 \le f_i < 16$),则 \begin{equation} v_i = F \left ( v_{a_i}, v_{b_i}, f_i \right ) = \left \lfloor \frac{f_i}{2 ^ {2 v_{a_i} + v_{b_i} }} \right \rfloor \mod 2 \end{equation} 我们称第 $i$ 只跳蚤依赖于第 $a_i$ 和第 $b_i$ 只跳蚤(注意$a_i$可以等于$b_i$)。
下面给出了几个关于 $F$ 的例子:
| $a$ | $b$ | $F(a,b,14)$ | $F(a,b,8)$ | $F(a,b,6)$ |
|---|---|---|---|---|
| $0$ | $0$ | $0$ | $0$ | $0$ |
| $0$ | $1$ | $1$ | $0$ | $1$ |
| $1$ | $0$ | $1$ | $0$ | $1$ |
| $1$ | $1$ | $1$ | $1$ | $0$ |
一开始(第 $0$ 时刻),所有编号小于 $2n$ 的跳蚤的值都同时被确定。 然后对于每只编号大于等于 $2n$ 的跳蚤, 它的值将在它依赖的跳蚤的值都确定之后立即开始确定。 由于跳蚤国的信息技术不发达, 每只跳蚤确定它的值需要1小时(注意多只跳蚤可以同时确定它们的值)。
下面是一个例子:(id表示编号,t表示该跳蚤的值被确定的时间,箭头表示跳蚤的依赖关系)
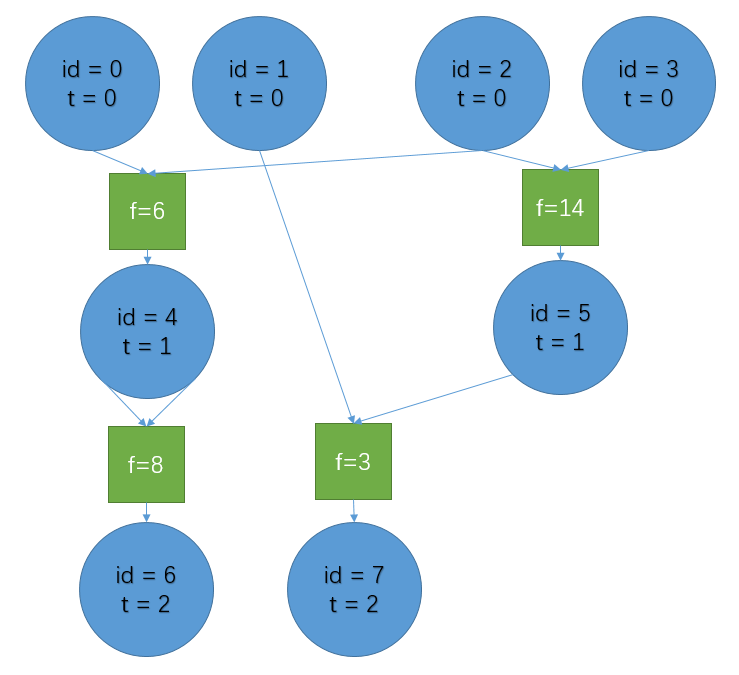
我们可以把编号小于 $2n$ 的跳蚤的值看作两个 $n$ 位的二进制数 $\mathrm{A}, \mathrm{B}$, 其中 $\mathrm{A} = (v_{n-1} \ v_{n-2} \ \cdots \ v_0)_2$, $\mathrm{B} = (v_{2n-1} \ v_{2n-2} \ \cdots \ v_{n})_2$。 跳蚤国王要对 $\mathrm{A}$ 和 $\mathrm{B}$ 做一些运算,得到一个 $n$ 位二进制数, 并用 $n$ 只跳蚤表示出来。
由于跳蚤国王还要带着跳蚤们去舞会,你能使用的跳蚤的数量和时间都有限。 具体来说,你最多使用 $\mathrm{M}$ 只跳蚤,并要求按顺序指定 $n$ 只跳蚤, 在 $\mathrm{T}$ 小时内,你使用的所有跳蚤的值都能被确定, 且指定的 $n$ 只跳蚤的值表示的二进制数为跳蚤国王所求的答案。
作为奖励,跳蚤国王打算送你一个UOJ抱枕。 第一个通过最后一个测试点的选手将获得一个UOJ抱枕。 如果没有选手通过最后一个测试点,则第一个得到此题最高分的选手将获得一个UOJ抱枕。
任务
你需要编写一个函数 build_computer,来帮助跳蚤国王造计算机。
build_computer(task_id, n, M, T)task_id: 子任务编号n: 输入的$\mathrm{A}$和$\mathrm{B}$的位数M: 除了编号小于$2n$的跳蚤之外,最多能使用的跳蚤的数目T: 你使用的所有跳蚤的值都要在$\mathrm{T}$小时内被确定
你可以调用一个函数 add_flea(a, b, f),
表示增加一只跳蚤,对于第 $i$ 次调用,
增加的跳蚤的编号为$2n + i - 1$,
$a_{2n+i-1}, b_{2n+i-1}, f_{2n+i-1}$分别被设置为$a, b, f$,
然后这个函数会返回$2n + i - 1$。
你最多能调用$\mathrm{M}$次 add_flea。
你还需要对每个 $[0, n-1]$ 中的整数 $i$ 调用 set_output 函数(可以按任意顺序调用)。
set_output(i, id) 表示设置输出的二进制数的第 $i$ 位为编号为 $id$ 的跳蚤的值。
子任务
| 子任务编号 | 需要计算的表达式 |
|---|---|
| 1 | $(\mathrm{A} + 1) \mod 2 ^ n$ |
| 2 | $(\mathrm{A} + \mathrm{B}) \mod 2 ^ n$ |
| 3 | $(\mathrm{A} \times \mathrm{B}) \mod 2 ^ n$ |
设 $m$ 为 add_flea 的调用次数,$t$ 为所有跳蚤的值被确定的最晚时刻。
| 测试点编号 | 子任务编号 | 分值 | $n$ | $\mathrm{M}$ | $\mathrm{T}$ | 备注 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | $1$ | $10000$ | $10000$ | |
| 2 | 1 | 2 | $2$ | $10000$ | $10000$ | |
| 3 | 1 | 5 | $256$ | $10000$ | $10000$ | |
| 4 | 1 | 9 | $10^5$ | $5 \times 10^5$ | $50$ | 该测试点得分为$\min \left \{ \left \lfloor \frac{5 \times 10^5 - m}{20000} \right \rfloor, 9 \right \}$分 |
| 5 | 1 | 10 | $10^5$ | $1.5 \times 10^6$ | $30$ | 该测试点得分为$\min \left \{30-t, 10 \right \}$分 |
| 6 | 2 | 3 | $2$ | $10000$ | $10000$ | |
| 7 | 2 | 6 | $233$ | $10000$ | $10000$ | |
| 8 | 2 | 13 | $10^5$ | $1.2 \times 10^6$ | $100$ | 该测试点得分为$\min \left \{ \left \lfloor \frac{1.2 \times 10^6-m}{30000} \right \rfloor, 13 \right \}$分 |
| 9 | 2 | 14 | $10^5$ | $5 \times 10^6$ | $42$ | 该测试点得分为$\min \left \{42-t, 14 \right \}$分 |
| 10 | 3 | 4 | $2$ | $10000$ | $10000$ | |
| 11 | 3 | 7 | $233$ | $10^6$ | $10^6$ | |
| 12 | 3 | 8 | $512$ | $3 \times 10^6$ | $255$ | |
| 13 | 3 | 17 | $1024$ | $4 \times 10^6$ | $94$ | 该测试点得分为$\min \left \{ \left \lfloor\frac{94-t}{2} \right \rfloor, 17 \right \}$分 |
| 14 | 3 | 1 | $1024$ | $1920000$ | $288$ |
实现细节
本题只支持C++。
你只能提交一个源文件实现如上所述的 build_computer 函数,并且遵循下面的命名和接口。
你需要包含头文件 king.h。
void build_computer(int task_id, int n, int M, int T);函数 add_flea 和 set_output 的接口信息如下。
int add_flea(int a, int b, int f);
void set_output(int i, int id);评测方式
评测系统将读入如下格式的数据:
- 第1行:子任务编号
- 第2行:$n, \mathrm{M}, \mathrm{T}$
如果你调用 add_flea 的次数大于 $\mathrm{M}$,
或调用 set_output的次数不等于 $n$,
或没有对 $[0, n-1]$ 中的每个整数作为 set_output 的第一个参数调用 set_output,
你的程序将被判为“Incorrect”。
在 build_computer 返回后,如果在 $\mathrm{T}$ 小时后,存在一只跳蚤的值还没被确定,则评测系统输出“Incorrect”,
否则我们将用若干组输入对你造的计算机进行测试,
如果对于所有输入数据,你的输出都正确,评测系统将输出“Correct”,否则输出“Incorrect”。
如果评测系统第一行输出了“Correct”,则第二行将会输出 $m$ 和 $t$(定义见“子任务”),否则会输出具体的错误信息。
时间限制:$1\texttt{s}$
空间限制:$512\texttt{MB}$
在任何时候,交互库使用的内存都不会超过$128\texttt{MB}$,即选手至少有$384\texttt{MB}$的可用内存。