曾经有一款流行的游戏,叫做 Infinity Loop,先来简单的介绍一下这个游戏:
游戏在一个 n×m 的网格状棋盘上进行,其中有些小方格中会有水管,水管可能在方格某些方向的边界的中点有接口,所有水管的粗细都相同,所以如果两个相邻方格的公共边界的中点都有接头,那么可以看作这两个接头互相连接。水管有以下 15 种形状:
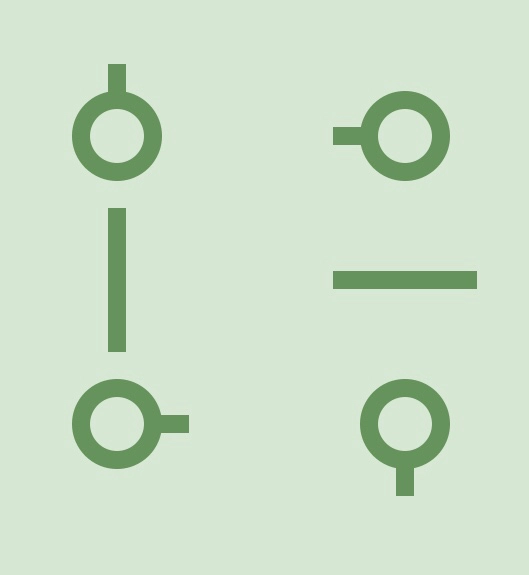

游戏开始时,棋盘中水管可能存在漏水的地方。
形式化地:如果存在某个接头,没有和其它接头相连接,那么它就是一个漏水的地方。
玩家可以进行一种操作:选定一个含有非直线型水管的方格,将其中的水管绕方格中心顺时针或逆时针旋转90度。
直线型水管是指左图里中间一行的两种水管。
现给出一个初始局面,请问最少进行多少次操作可以使棋盘上不存在漏水的地方。
输入格式
从标准输入读入数据。
第一行两个正整数 n,m,代表网格的大小。
接下来 n 行每行 m 个数,每个数是 [0,15] 中的一个,你可以将其看作一个 4 位的二进制数,从低到高每一位分别代表初始局面中这个格子上、右、下、左方向上是否有水管接头。
特别地,如果这个数是 0 ,则意味着这个位置没有水管。
比如 3(0011(2)) 代表上和右有接头,也就是一个L型,而 12(1100(2)) 代表下和左有接头,也就是将L型旋转180度。
输出格式
输出到标准输出。
输出共一行,表示最少操作次数。如果无法达成目标,输出-1.
样例一
input
2 3
3 14 12
3 11 12output
2explanation
样例1棋盘如下

旋转方法很显然,先将左上角虚线方格内的水管顺时针转90度
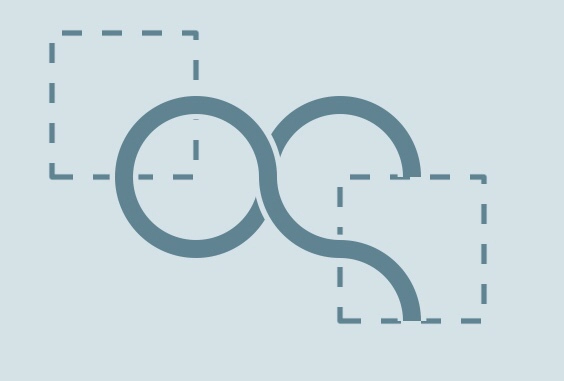
然后右下角虚线方格内的水管顺时针旋转90度,这样就使得水管封闭了
样例二
input
3 2
1 8
5 10
2 4output
-1explanation
样例2为题目描述中的第一张图片,无法达成目标。
样例三
input
3 3
9 11 3
13 15 7
12 14 6output
16explantion
样例3为题目描述中的第二张图片,将除了中心方格以外的每个方格内的水管都转180度即可。
限制与约定
| 测试点编号 | n+m的范围 | 特殊约定 |
|---|---|---|
| 1 | nm≤16 | 无特殊要求 |
| 2 | ||
| 3 | nm≤2000 | min |
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | 无特殊要求 | |
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 | ||
| 15 | ||
| 16 | ||
| 17 | ||
| 18 | ||
| 19 | ||
| 20 |