题面描述
一棵以1为根的树,一共 $n$ 个节点,每一个节点都有颜色,初始时颜色编号都为 1 。
一共进行 $m$ 次操作,操作有两种:
1 x y:把以 $x$ 为根的子树的全部节点染成 $y$ 号颜色。2 x:询问把连接不同颜色的点的边删掉后,$x$ 所在的连通块大小。边不实际删掉。
输入格式
第一行一个整数 $n$ 。
接下来 $n-1$ 行描述这棵树,每行两个整数 $u,v$ ,表示树上的一条边。
第 $n+1$ 行一个整数 $m$ 。
接下来 $m$ 行,每行一个操作,格式如题面所述。
输出格式
对于每一个操作2,输出一行一个整数表示答案。
样例一
input
5 1 2 1 3 2 4 2 5 5 2 2 1 3 2 2 1 1 4 2 2 5
output
5 4 3
explanation
我们用红色表示1,绿色表示2,这是初始的各点颜色,此时询问节点2的答案是5:
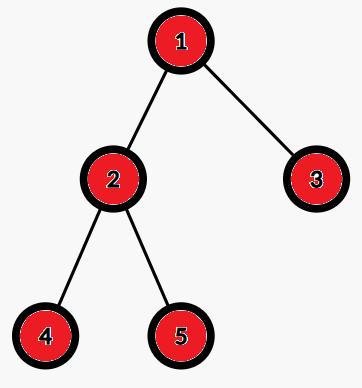
这是第一次修改后的树,此时询问节点1的答案是4:
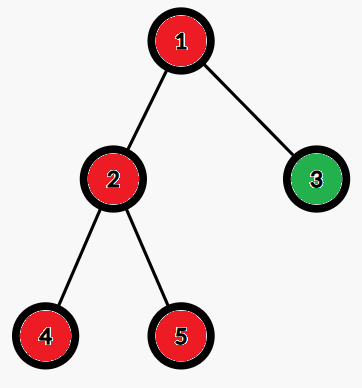
这是第二次修改后的树,此时询问节点5的答案是3:
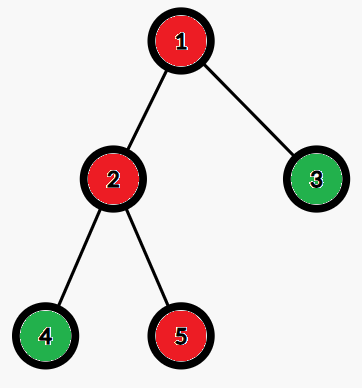
样例二
input
10 1 2 2 3 1 4 2 5 3 6 2 7 6 8 8 9 9 10 15 1 4 10 1 2 4 1 1 5 1 7 10 1 8 10 2 8 2 2 1 1 5 1 3 4 1 9 9 1 4 6 2 6 2 1 1 4 4 2 2
output
3 6 3 4 4
限制与约定
对于所有数据,$1\leq n\leq 10^6$ ,$1\leq m \leq 10^6$ ,$1\leq y\leq n$ 。
| 测试点编号 | $n\leq$ | $m\leq$ | 特殊限制 |
|---|---|---|---|
| 1~6 | $10^5$ | $10^6$ | $n\times m\leq10^8$ |
| 7~10 | $10^5$ | 无 | |
| 11~12 | $10^6$ | $10^6$ | 点 $i$ 的父亲在 $[1,i-1]$ 以内随机生成(点1除外) |
| 13~14 | $5\times10^5$ | $5\times10^5$ | 无 |
| 15 | $10^6$ | $10^6$ | 点 $i$ 的父亲是 $i-1$(点1除外) |
| 16~20 | 无 |
时间限制:2s
空间限制:1024MB