小 L 作为一名 OIER,做过了广为人知的棋盘计数问题。
即,给定一个无限大的棋盘,第 i 行第 j 列记作位置 (i,j),棋盘上有若干个位置被标记,棋子只能经过被标记的地方,保证 (1,1) 被标记,有一颗棋子初始在 (1,1),每次只能向右或向下(即将某一位的坐标增加 1),对于所有位置求出有多少种方案可以走到这里。
然而小 L 觉得太简单了,记走到 (i,j) 位置的方案数为 fi,j(如果无法走到该位置则 fi,j=0),他希望选出若干个不同位置,使得它们的 f 值加起来等于给定的数 k,如果有多种方案,任意输出一种即可,小 L 会询问 Q 次。
小 L 希望每次询问选出的位置尽量的少,同时,小 L 希望棋盘上被标记的位置也尽量的少,请你构造一组方案来满足条件。
具体的,小 L 希望棋盘上被标记的位置不超过 X,每次询问选择的位置数不超过 Y。
输入格式
第一行三个正整数,分别为 K,Q,X,Y,保证询问的所有 k 满足 1≤k<10K。
接下来 Q 行,每行一个整数 k。
输出格式
第一行一个正整数 n,表示棋盘上被标记的数的数量,你需要保证 n≤X。
接下来 n 行,每行两个数 x,y,表示被标记的位置的坐标,你需要保证被标记的坐标互不相同,并且你需要注意这里的输出顺序(后续需要考虑),尽管棋盘是无限大的,你还是需要保证输出的坐标 x,y 满足 1≤x,y≤n。
接下来 Q 行,每行一个长度为 n 的 01 串,其中第 i 位为 1 表示你选择了第 i 个被标记的坐标。
你需要保证 n≤X,并且 01 串中 1 的数量不超过 Y。
输入输出样例
样例输入
2 3 1000 340
1
2
3
样例输出
8
1 1
1 2
1 3
2 1
2 3
3 1
3 2
3 3
10000000
00000110
10000001
样例解释
棋盘如下:
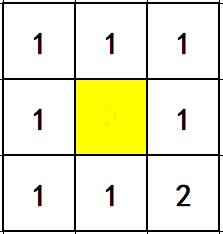
其中左上角为格子 (1,1),右下角为 (3,3),黄色格子是未被标记的格子,格子中的数为对应的 f 值,当然棋盘大小不止 3×3,这里只展示了存在被标记的格子的区域。
第一次询问选择了格子 (1,1),第二次询问选择了格子 (3,1),(3,2),第三次询问选择了格子 (1,1),(3,3)。
下发文件中提供了 checker.cpp,你可以将其编译成可执行文件,其使用格式为 checker chess.in chess.out,其中 chess.in 为输入文件,chess.out 为你的输出,checker 会执行检查命令并返回错误所对应的编码:
- 输出格式出错(包括 n>X 但不包括 01 串中 1 的数量 >Y)
- 01 串中 1 的数量 >Y。
- 你所构造的方案的 f 值之和不是询问所需要的值。
如果你的构造正确,checker 会返回 correct。
你可以参考或直接使用 checker 提供的高精度模板。
注意下发 checker 和实际 checker 有所不同。
数据范围
| Subtask | 分值 | X= | Y= | K= | 特殊性质 |
|---|---|---|---|---|---|
| 1 | 5 | 103 | 340 | 2 | 无 |
| 2 | 10 | 103 | 340 | 12 | 无 |
| 3 | 10 | 103 | 340 | 100 | 无 |
| 4 | 10 | 990 | 310 | 100 | 数据随机 |
| 5 | 10 | 1050 | 260 | 100 | 无 |
| 6 | 10 | 1050 | 240 | 100 | 无 |
| 7 | 15 | 980 | 260 | 100 | Q=1 |
| 8 | 30 | 960 | 240 | 100 | 无 |
其中,数据随机的方式是:k 在 [1,10K) 中等概率随机。
对于所有数据,保证 1≤Q≤104。