给定一张 n 个点,m 条边的带权有向图,这张图的每条边两个端点在 n 个顶点中均匀随机生成,边权在 [0,232) 中均匀随机生成,且上述随机独立。
再给定 q 组询问,每组询问给定两个端点 si,ti,你需要给出从 si 出发到达 ti 的路径边权和最小值,如果不存在这样的路径,请输出 −1。
我们保证 q 组询问的 si,ti 是在所有顶点中均匀独立随机的,且与图的生成也独立。
请注意,点的编号为 1∼n,且图中可能生成重边与自环。
Input
第一行四个整数 n,m,q,seed,其中 seed 是在 [0,232) 中均匀随机选取的整数,用于生成图。选手可以根据题目结尾的代码生成所需图。
下面 q 行,每行两个正整数 si,ti 表示一组询问。
我们保证 q 组询问的 si,ti 是在所有顶点中均匀独立随机的,且与图的生成也独立。
Output
一共 q 行,每行一个整数表示答案。
Example
Input
4 8 5 1112792816 2 3 4 3 4 3 3 2 1 4
Output
3419197189 1798364963 1798364963 3986398077 2337967903
Notes
这是样例对应的图:
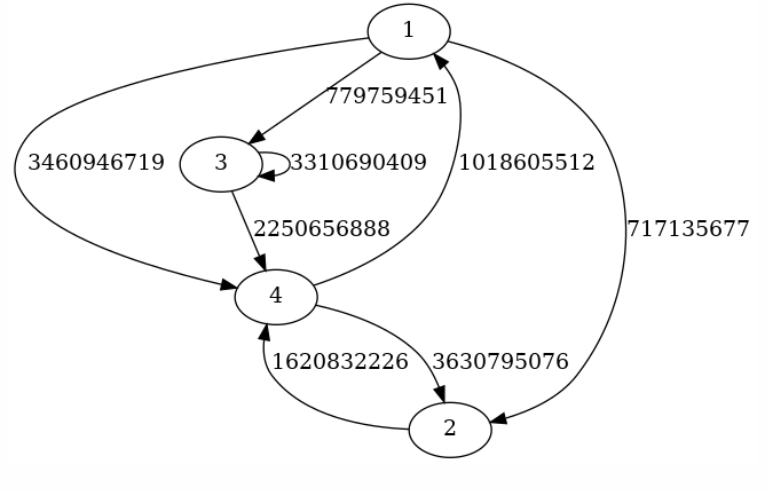
对于所有数据:1≤n≤2×105,1≤m≤3×106,1≤q≤104。
| 子任务编号 | 数据范围 | 分值 |
|---|---|---|
| 1 | n,m,q≤2×103 | 5 |
| 2 | n≤3×103 | 15 |
| 3 | m≤n | 10 |
| 4 | m≤2.5×n | 20 |
| 5 | m≤5×105 | 20 |
| 6 | n≤105 | 10 |
| 7 | 无 | 20 |
图生成器:
#include<tuple>
#include<vector>
#include<random>
std::vector<std::tuple<int, int, long long>> generate_edges(int n, int m, unsigned seed) {
std::mt19937 gen(seed);
std::vector<std::tuple<int, int, long long>> edges(m);
unsigned max = -1u / n * n;
auto sample = [&]() {
unsigned x;
do { x = gen(); } while(x >= max);
return x % n + 1;
};
for(auto & [u, v, w] : edges) {
u = sample();
v = sample();
w = gen();
} // u 到 v 存在边权为 w 的边
return edges;
}如果你不理解这段代码,你可以认为 mt19937 是一个比较强的伪随机数生成器,由这段代码生成的图在正常情况下可以认为是独立均匀随机生成的图,它以 tuple 的方式存储了一条边,并用 vector 存储了 m 条边并返回。