问题描述
某校由于历史悠久,校园中有大量的名胜古迹。为了更好地保护这些古迹,学校决定用篱笆将这些古迹围起来。
现在已知有 $p$ 个地点的古迹需要保护。这些古迹可以看做二维平面上的整数点。有 $n$ 个点可以作为篱笆的端点,这些端点的坐标也为二维平面上的整数。端点用 $1$ 到 $n$ 的整数编号。
有 $m$ 对端点之间可以修建篱笆。用 $(u,v,w)$ 描述一段可以修建的篱笆,表示端点 $u$ 和端点 $v$ 之间可以花费 $w$ 的代价修建一段。篱笆都看做直线段。为了方便设计,这些可以修建的篱笆都是不会相交的(只会在端点处相交)。
将一个古迹围起来是指存在一个由篱笆构成的简单多边形,这个古迹在该多边形内部。
由于经费问题,学校希望修建篱笆的花费最小。你需要输出将至少 $1$ 个,$2$ 个,…,$p$ 个古迹围起来的最小花费。
输入格式
第一行包含三个正整数 $p$, $n$, $m$ 表示古迹的个数,端点个数和可以修建的篱笆条数。
接下来 $p$ 行,每行包含两个整数,表示每个古迹的坐标。
接下来 $n$ 行,每行包含两个整数,表示每个端点的坐标。这些端点按照输入的顺序依次用 $1$ 到 $n$ 的整数编号。
最后 $m$ 行,每行包含三个非负整数 $u$, $v$, $w$,表示可以在端点 $u$ 和端点 $v$ 之间花 $w$ 的代价修建一段篱笆。
输出格式
输出 $p$ 行,分别表示将至少 $1$ 个,$2$ 个,…,$p$ 个古迹围起来的最小花费。
样例输入
3 9 15
-2 2
2 1
2 -1
3 0
3 2
1 2
-1 3
-3 3
-2 1
1 0
2 -2
2 -3
1 2 20
1 7 40
1 8 10
1 9 100
2 3 50
3 4 1000
3 7 10
4 5 10
4 6 10
4 7 1000
5 6 10
6 7 1000
7 8 120
7 9 10
8 9 10样例输出
30
100
140样例说明
样例如下图
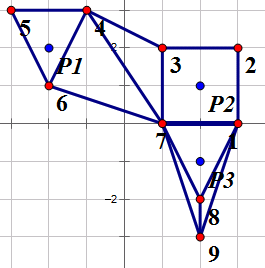
保护至少1个古迹的方案
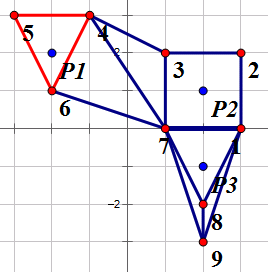
保护至少2个古迹的方案
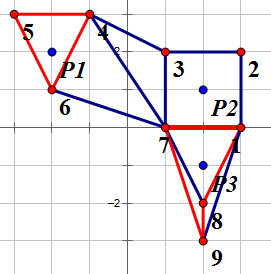
保护至少3个古迹的方案
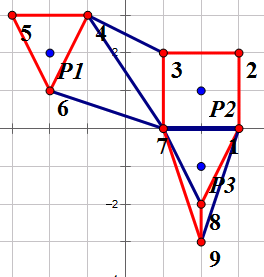
数据规模及约定
对于 $100\%$ 的数据,$n\leq 100$, $m \leq \binom{n}{2}$,$p\leq 10$。所有坐标位置的两维绝对值不超过 $10^9$,$u,v$ 不超过 $n$,$w$ 不超过 $10^6$。
保证可以修建的篱笆不会经过古迹。保证可以修建的两段篱笆不会在非端点处相交或重合。保证至少存在一种方案可以包围所有古迹。保证 $n$ 个点互不相同。
具体每组数据的规模如下
| 编号 | $n$ | $p$ | 编号 | $n$ | $p$ |
| 1 | 50 | 1 | 6 | 100 | 8 |
| 2 | 100 | 1 | 7 | 100 | 9 |
| 3 | 15 | 3 | 8 | 50 | 10 |
| 4 | 40 | 4 | 9 | 80 | 10 |
| 5 | 100 | 6 | 10 | 100 | 10 |