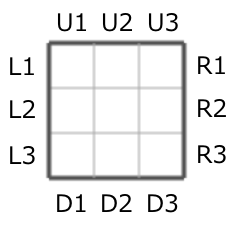
小 T 有一张 n×n 的棋盘和很多硬币。他想把硬币都放到棋盘上,使得每个格子上恰好有一枚硬币。 记棋盘第一行的上方从左到右的位置依次为 U1,U2,⋯,Un,最后一行下方从左到右的位置依次为 D1,D2,⋯,Dn。类似地,记第一列左边和最后一列右边从上到下的位置依次分别为 L1,L2,⋯,Ln 与 R1,R2,⋯,Rn。
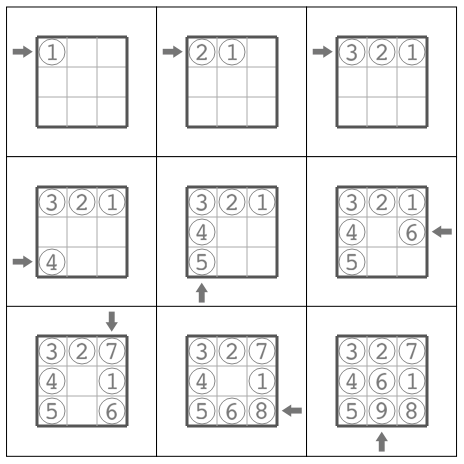
每次操作,小 T 会将一枚硬币放在这些在棋盘外面且与某个格子相邻的位置,之后按照往棋盘内的方向推硬币,直到该枚硬币恰好位于格子内为止。若格子上已经有另外一枚硬币,则那枚硬币也会被往里推一个格子。如果有硬币被推出棋盘外则视为失败。例如,下图是在 3×3 的棋盘上进行的 9 次合法操作。
小 T 觉得这样推硬币还是太没意思了。于是他对每个棋盘外面的位置 Ui,Di,Li,Ri 都分别写上了数 Ui,Di,Li,Ri,表示在这个位置进行操作的次数。但在写完数之后,小 T 发现他并不能很快找出一组合法的方案,你能帮他找到吗?
输入格式
第一行一个整数 n,表示棋盘大小。
第二行 n 个整数 Ui,表示位置 Ui 的操作次数。
第三行 n 个整数 Di,表示位置 Di 的操作次数。
第四行 n 个整数 Li,表示位置 Li 的操作次数。
第五行 n 个整数 Ri,表示位置 Ri 的操作次数。
输出格式
如果无解,输出 NO。
否则输出 n2 行,每行形如 Ui,Di,Li 或 Ri,表示该次操作的位置。
样例输入 1
3 0 0 1 1 1 0 3 0 1 0 1 1
样例输出 1
L1 L1 L1 L3 D1 R2 U3 R3 D2
样例输入 2
2 3 0 0 0 0 1 0 0
样例输出 2
NO
样例解释
样例 1 即为题面中所给图片。
样例 2 中 U1=3,显然不可能构造出合法方案。
数据范围
对于所有数据,1≤n≤300,0≤Ui,Di,Li,Ri,∑(Ui+Di+Li+Ri)=n2。
子任务 1(11 分):n≤3。
子任务 2(15 分):Di=Ri=0。
子任务 3(19 分):Di=0。
子任务 4(25 分):n≤40。
子任务 5(30 分):无特殊限制。